Jednym z zadań w podstawie programowej z informatyki, jest sprawdzanie przynależności punktu do odcinka. Dzisiaj spróbujemy pokonać ten temat.
Wstępne założenia
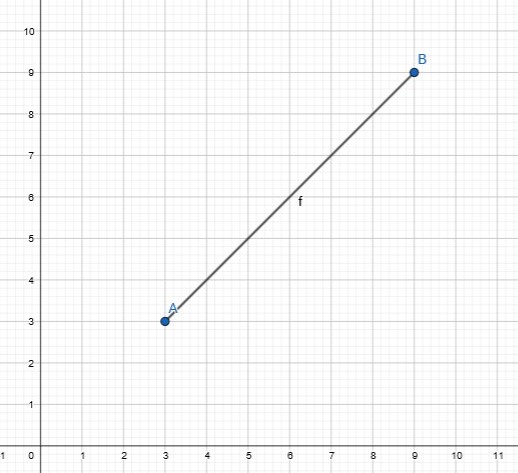
Na początek załóżmy, że mamy trzy punkty w przestrzeni dwuwumiarowej XY (przestrzeń euklidesowa o wymiarze 2) – punkt ![]() , punkt
, punkt ![]() i punkt
i punkt ![]() . Dwa pierwsze punkty tworzą odcinek
. Dwa pierwsze punkty tworzą odcinek ![]() . Na przykład dla A(3,3) i B(9,9)
. Na przykład dla A(3,3) i B(9,9)
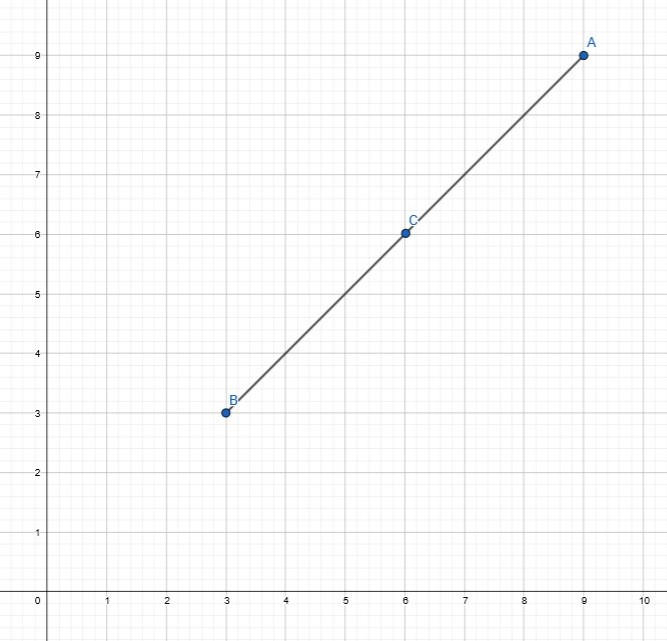
Wyobraźmy sobie teraz punkt C i jego możliwe położenia:
- Punkt C może leżeć na odcinku (np. C(6,6) )

- Punkt C może leżeć na prostej przechodzącej przez odcinek, ale poza krańcami odcinka (np. C(2,2) lub C(10,10) )
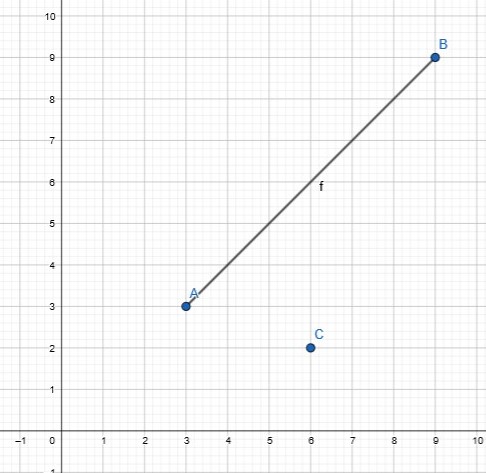
- Punkt C może leżeć całkowicie poza odcinkiem (np. C(6,2) )
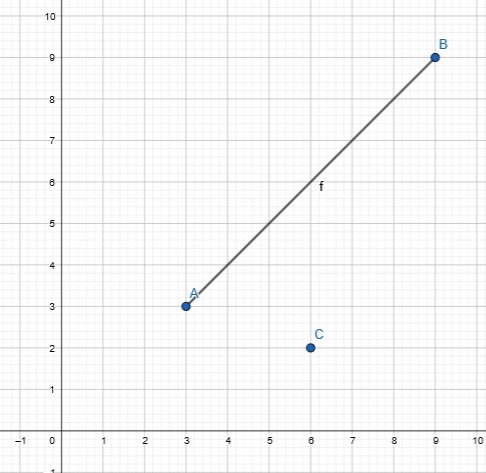
Zadaniem programu, który napiszemy, jest sprawdzenie czy punkt należy do odcinka, czyli czy zachodzi pierwszy przypadek.
Wczytywanie danych od użytkownika
Na początek należy wczytać dane od użytkownika. Na potrzeby tego zadania założę, że program prowadzi dialog z użytkownikiem i wczytuje dane z konsoli tekstowej.
Java
import java.util.Scanner;
public class PolozeniePunktu {
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
System.out.print("Punkt A. Podaj x: ");
double xa = s.nextDouble();
System.out.print("Punkt A. Podaj y: ");
double ya = s.nextDouble();
System.out.print("Punkt B. Podaj x: ");
double xb = s.nextDouble();
System.out.print("Punkt B. Podaj y: ");
double yb = s.nextDouble();
System.out.print("Punkt C. Podaj x: ");
double xc = s.nextDouble();
System.out.print("Punkt C. Podaj y: ");
double yc = s.nextDouble();
s.close();
}
}
C++
#include <iostream>;
using namespace std;
int main()
{
double xa, xb, xc, ya, yb, yc;
cout << "Punkt A. Podaj x: "; cin >> xa;
cout << "Punkt A. Podaj y: "; cin >> ya;
cout << "Punkt B. Podaj x: "; cin >> xb;
cout << "Punkt B. Podaj y: "; cin >> yb;
cout << "Punkt B. Podaj x: "; cin >> xc;
cout << "Punkt C. Podaj y: "; cin >> yc;
return 0;
}
Python
print("Punkt A. Podaj x: ",end='')
xa = float(input())
print("Punkt A. Podaj y: ",end='')
ya = float(input())
print("Punkt B. Podaj x: ",end='')
xb = float(input())
print("Punkt B. Podaj y: ",end='')
yb = float(input())
print("Punkt C. Podaj x: ",end='')
xc = float(input())
print("Punkt C. Podaj y: ",end='')
yc = float(input())
Badanie współiniowości punktów
Na samym początku odrzucimy przypadek, w którym punkt C leży nie tylko poza odcinkiem, ale także leży poza prostą przechodzącą przez odcinek, czyli sprawdzimy czy wszystkie 3 punkty są współliniowe (leżą na jednej prostej). To za mało, żeby stwierdzić, że punkt C należy do odcinka |AB|, ale to już pierwszy krok.
Macierz i jej wyznacznik
Aby zbadać współliniowość punktów, musimy wprowadzić pojęcie macierzy oraz jej wyznacznika. Szerzej zapewne zapoznasz się z tymi pojęciami na matematyce, tu tylko proste wyjaśnienie.
Macierz to układ liczb (albo symboli) ułożonych w wiersze i kolumny. W matematyce i informatyce używana jest bardzo często, choćby do rozwiązywania układów równań czy dokonywania przekształceń geometrycznych (np. w grach komputerowych). W tym zadaniu posłuży do zbadania czy nasze punkty leżą na jednej prostej.
W tym celu należy zbudować macierz 3×3 o następującym wyglądzie:
![Rendered by QuickLaTeX.com \[ \mathbf{M} = \left[ \begin{array}{ccc} x_{a} & y_{a} & 1 \\ x_{b} & y_{b} & 1 \\ x_{c} & y_{c} & 1 \\ \end{array} \right] \]](https://edukacja.gwarantowana.pl/wp-content/ql-cache/quicklatex.com-ded8918a7942a27e8627ef5063133863_l3.png)
Jedynki w trzeciej kolumnie są wynikiem tego, że tak naprawdę posługujemy się trójwymiarową przestrzenią i nasze punkty brutalnie sprowadziliśmy do dwóch wymiarów.
I teraz mamy matematyczne twierdzenie: Jeżeli wyznacznik tej macierzy wynosi zero, to znaczy że punkty leżą na wspólnej prostej. Wystarczy więc wyliczyć ów wyznacznik, porównać z zerem i odpowiedź jest. Ale co to jest wyznacznik macierzy oraz jaką ma wartość?
W przypadku macierzy 3×3, z jaką mamy do czynienia, obliczanie wyznacznika jest bardzo proste. Należy przepisać dwa pierwsze wiersze pod macierzą i stworzyć taką wydłużoną macierz:
![Rendered by QuickLaTeX.com \[ \mathbf{M} = \left[ \begin{array}{ccc} x_{a} & y_{a} & 1 \\ x_{b} & y_{b} & 1 \\ x_{c} & y_{c} & 1 \\ x_{a} & y_{a} & 1 \\ x_{b} & y_{b} & 1 \\ \end{array} \right] \]](https://edukacja.gwarantowana.pl/wp-content/ql-cache/quicklatex.com-c14c8bc14161489c34ae9f762f71a548_l3.png)
Możemy teraz wyodrębnić trzy trójki na przekątnej:
![Rendered by QuickLaTeX.com \[ \mathbf{M} = \left[ \begin{array}{ccc} \mathbf{x_{a}} & y_{a} & 1 \\ x_{b} & \mathbf{ y_{b}} & 1 \\ x_{c} & y_{c} & \mathbf{1} \\ x_{a} & y_{a} & 1 \\ x_{b} & y_{b} & 1 \\ \end{array} \right] \mathbf{M} = \left[ \begin{array}{ccc} x_{a} & y_{a} & 1 \\ \mathbf{x_{b}} & y_{b} & 1 \\ x_{c} & \mathbf{y_{c}} & 1 \\ x_{a} & y_{a} & \mathbf{1} \\ x_{b} & y_{b} & 1 \\ \end{array} \right] \mathbf{M} = \left[ \begin{array}{ccc} x_{a} & y_{a} & 1 \\ x_{b} & y_{b} & 1 \\ \mathbf{x_{c}} & y_{c} & 1 \\ x_{a} & \mathbf{y_{a}} & 1 \\ x_{b} & y_{b} & \mathbf{1} \\ \end{array} \right] \]](https://edukacja.gwarantowana.pl/wp-content/ql-cache/quicklatex.com-0ea4731fdc19683c5638cb78c4653c34_l3.png)
I analogicznie mamy trzy trójki na przeciwprzekątnej:
![Rendered by QuickLaTeX.com \[ \mathbf{M} = \left[ \begin{array}{ccc} x_{a} & y_{a} & \mathbf{1} \\ x_{b} & \mathbf{y_{b}} & 1 \\ \mathbf{x_{c}} & y_{c} & 1 \\ x_{a} & y_{a} & 1 \\ x_{b} & y_{b} & 1 \\ \end{array} \right] \mathbf{M} = \left[ \begin{array}{ccc} x_{a} & y_{a} & 1 \\ x_{b} & y_{b} & \mathbf{1} \\ x_{c} & \mathbf{y_{c}} & 1 \\ \mathbf{x_{a}} & y_{a} & 1 \\ x_{b} & y_{b} & 1 \\ \end{array} \right] \mathbf{M} = \left[ \begin{array}{ccc} x_{a} & y_{a} & 1 \\ x_{b} & y_{b} & 1 \\ x_{c} & y_{c} &\mathbf{1} \\ x_{a} & \mathbf{y_{a}} & 1 \\ \mathbf{x_{b}} & y_{b} & 1 \\ \end{array} \right] \]](https://edukacja.gwarantowana.pl/wp-content/ql-cache/quicklatex.com-1574594c15a2e9d2edf0802c57a56fd9_l3.png)
Wyznacznik macierzy M, oznaczany jako |M|, oznacza sumę iloczynów trójek na przekątnej od której odejmuje się sumę trójek na przeciwprzekątnej. Dla macierzy większego wymiaru nie jest już tak prosto i liczenie wyznaczników spędza sen z powiek studentów, jednak wymiar 3×3 jest łatwy, jak widać.
Ostatecznie otrzymujemy więc wzór:
![]()
Oczywiście jedynki można w tym mnożeniu pominąć
![]()
Do programu dopisujemy więc warunek:
Java
double wyznacznik = xa*yb+xb*yc+xc*ya-yb*xc-yc*xa-ya*xb;
if( wyznacznik == 0) {
// tu będziemy sprawdzać czy punkt nie leży poza krańcami odcinka
} else System.out.println("Niestety, punkt C nie leży na tym odcinku. :(");
C++
double wyznacznik = xa*yb+xb*yc+xc*ya-yb*xc-yc*xa-ya*xb;
if( wyznacznik == 0) {
// tu będziemy sprawdzać czy punkt nie leży poza krańcami odcinka
} else cout << "Niestety, punkt C nie leży na tym odcinku. :(");
Python
wyznacznik = xa*yb+xb*yc+xc*ya-yb*xc-yc*xa-ya*xb;
if wyznacznik == 0:
pass #tu będziemy sprawdzać czy punkt nie leży poza krańcami odcinka
else:
print("Niestety, punkt C nie leży na tym odcinku. :(")
Czy punkt leży na odcinku?
W ten sposób dotarliśmy do ostatniego sprawdzenia. Wiadomo już, że punkt leży na prostej przebiegającej przez odcinek, jednak jeszcze istnieje możliwość, że nie wewnątrz odcinka.
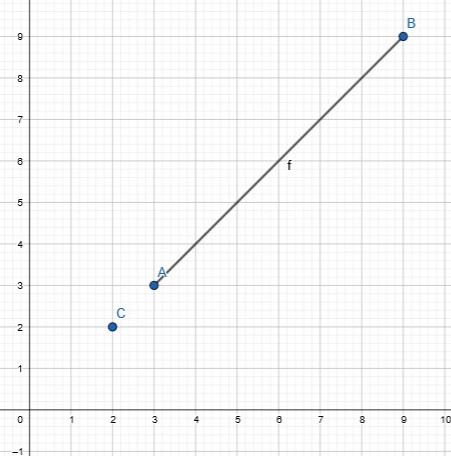
Spójrz jeszcze raz na rysunek z początku artykułu:
Jeżeli punkt C leży na odcinku |AB| to znaczy, że jego współrzędna x jest większa od współrzędnej x punktu A oraz mniejsza od współrzędnej punktu B. Chyba że odcinek wygląda tak:
Wtedy oczywiście współrzędne C muszą być większe od B i mniejsze od A. Skoro więc nie wiadomo jaki zwrot ma wektor AB, przyjmiemy następujące warunki:
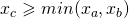 oraz
oraz 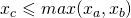
- oraz
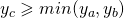 oraz
oraz 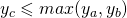
Zwróć uwagę na to, że zastosowałem ![]() oraz
oraz ![]() , bo przecież punkt C może leżeć dokładnie w jednym z końców odcinka.
, bo przecież punkt C może leżeć dokładnie w jednym z końców odcinka.
Uzupełnione sprawdzanie wygląda więc tak:
Java
double wyznacznik = xa*yb+xb*yc+xc*ya-yb*xc-yc*xa-ya*xb;
if( wyznacznik == 0) {
if( (xc >= Math.min(xa, xb)) && (xc <= Math.max(xa, xb)) && (yc >= Math.min(ya, yb)) && (yc >= Math.max(ya, yb)) ) System.out.println("C leży na |AB|");
else System.out.println("C nie leży na |AB| choć leżą na jednej prostej");
} else System.out.println("Niestety, punkt C nie leży na tym odcinku. :(");
C++
double wyznacznik = xa*yb+xb*yc+xc*ya-yb*xc-yc*xa-ya*xb;
if( wyznacznik == 0)
{
if( (xc <= min(xa, xb)) && (xc <= max(xa, xb)) && (yc >= min(ya, yb)) && (yc <= max(ya, yb)) ) cout << "C leży na |AB|" << endl;
else cout << "C nie leży na |AB| choć leżą na jednej prostej" << endl;
}
else cout << "Niestety, punkt C nie leży na tym odcinku. :(" << endl;
Python
Pamiętaj, że w Pythonie ważne są wcięcia.
wyznacznik = xa*yb+xb*yc+xc*ya-yb*xc-yc*xa-ya*xb;
if wyznacznik == 0:
if (xc >= min(xa, xb)) and (xc <= max(xa, xb)) and (yc >= min(ya, yb)) and (yc <= max(ya, yb)):
print("C leży na |AB|")
else:
print("C nie leży na |AB| choć leżą na jednej prostej")
else:
print("Niestety, punkt C nie leży na tym odcinku. :(")